| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
- AQE
- SQL
- redshift
- DataFrame Hint
- Spark Caching
- topic
- backfill
- CI/CD
- spark executor memory
- Salting
- Docker
- Speculative Execution
- Spark Partitioning
- mysql
- Spark 실습
- off heap memory
- colab
- Airflow
- Kubernetes
- aws
- Kafka
- Dag
- etl
- disk spill
- 데이터 파이프라인
- Spark
- 빅데이터
- KDT_TIL
- k8s
- Spark SQL
- Today
- Total
JUST DO IT!
머신 러닝을 위한 기초 선형 대수 알아보기 - TIL230718 본문
📚 KDT WEEK 16 DAY 2 TIL
- 기초 선형 대수
행렬 표기법

파이썬에서 numpy로 행렬 사용하기
import numpy as np
x = np.array([10.5, 5.2, 3.25, 7.0]) # 일차 배열
# 이차원화
x_2dims = np.expand_dims(x, axis=1)
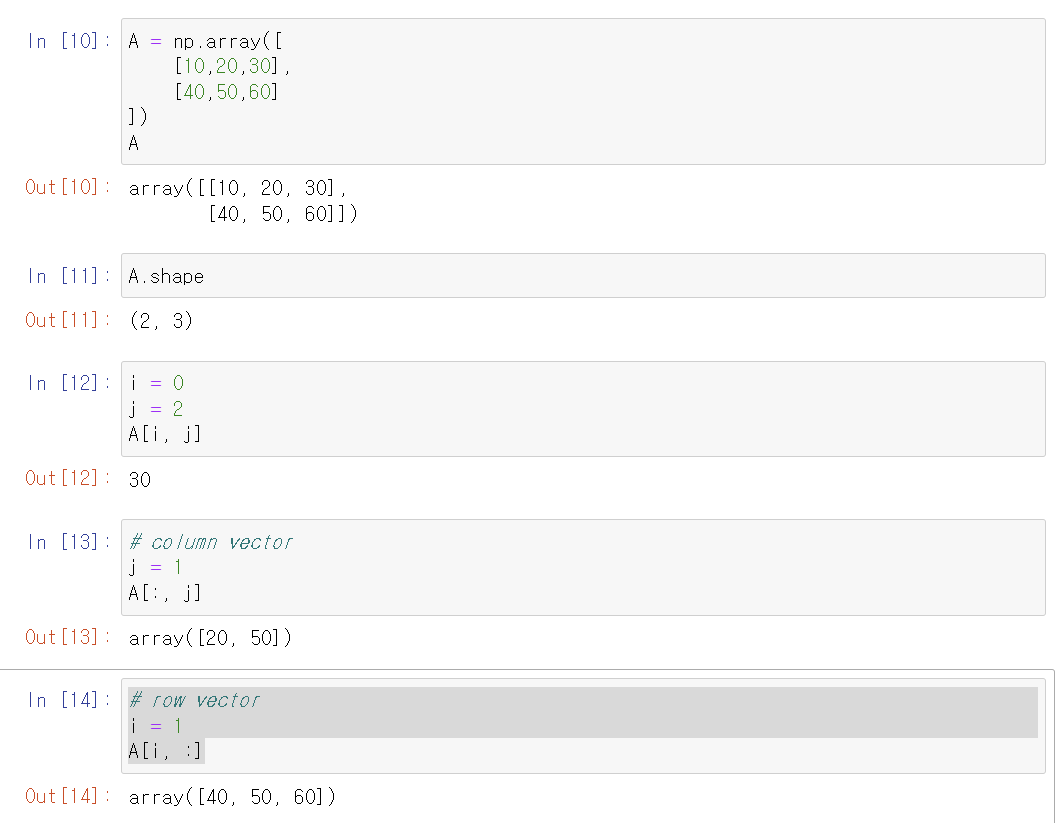
.shape를 사용하면 행렬의 형태를 알 수있고, 파이썬에서 배열다루듯 요소를 꺼내쓰면 된다.

이차배열로 선언해서 사용도 가능하고, 해당하는 행이나 열의 배열을 가져올 수 있다.
A = np.array([
[10,20,30],
[40,50,60]
])
# column vector
j = 1
A[:, j]
# row vector
i = 1
A[i, :]
결과
행렬의 곱셈
딥러닝에서 Neural Network의 주 계산 방법으로, 딥러닝을 공부한다면 이 행렬의 곱셈 이해가 필요하다.
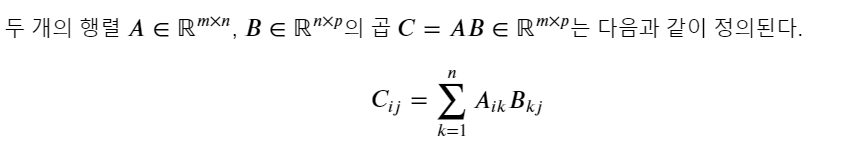
1. 벡터 x 벡터
1) 내적(inner product)

하나의 실수값이 결과값으로 리턴

2) 외적(outer product)
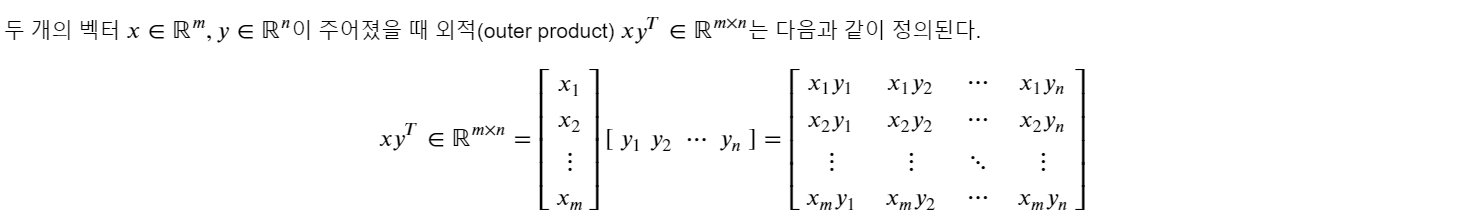
하나의 행렬값이 결과값으로 리턴
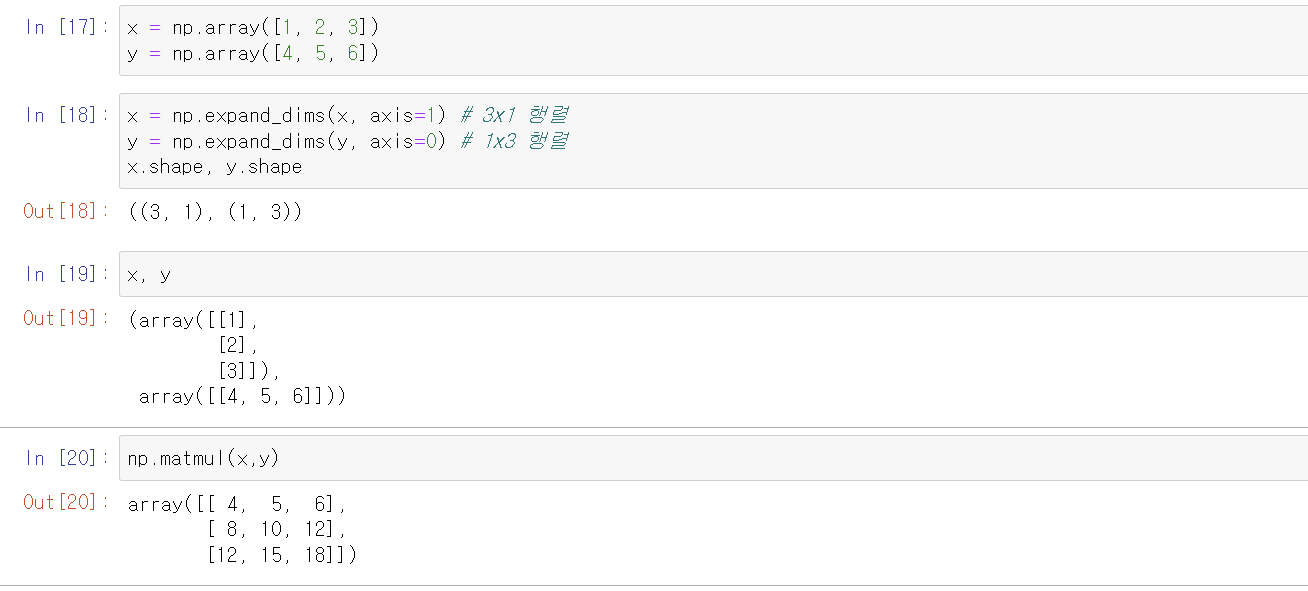
외적을 이용하면 모든 열이 동일한 값을 가진 행렬 A를 단순하게 표현할 수 있다.

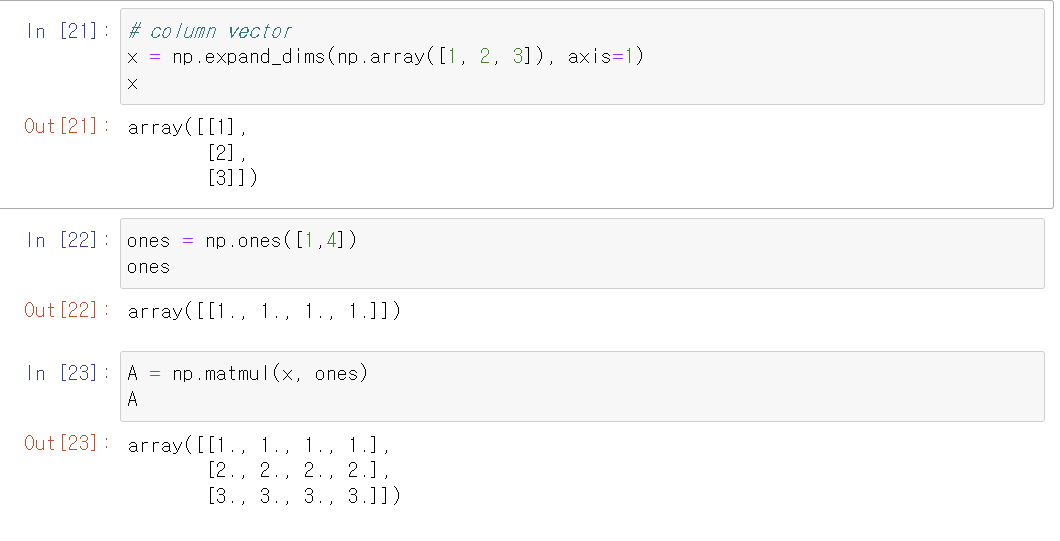
2. 행렬 x 벡터
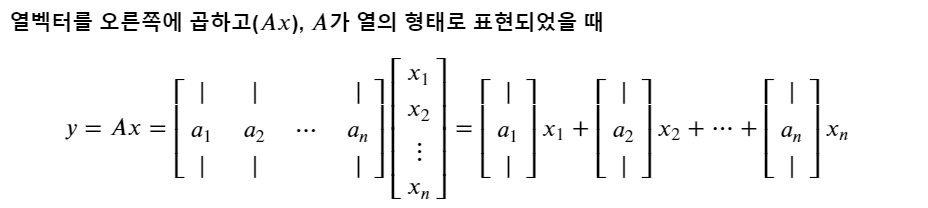
1) 열벡터를 오른쪽에 곱할 때

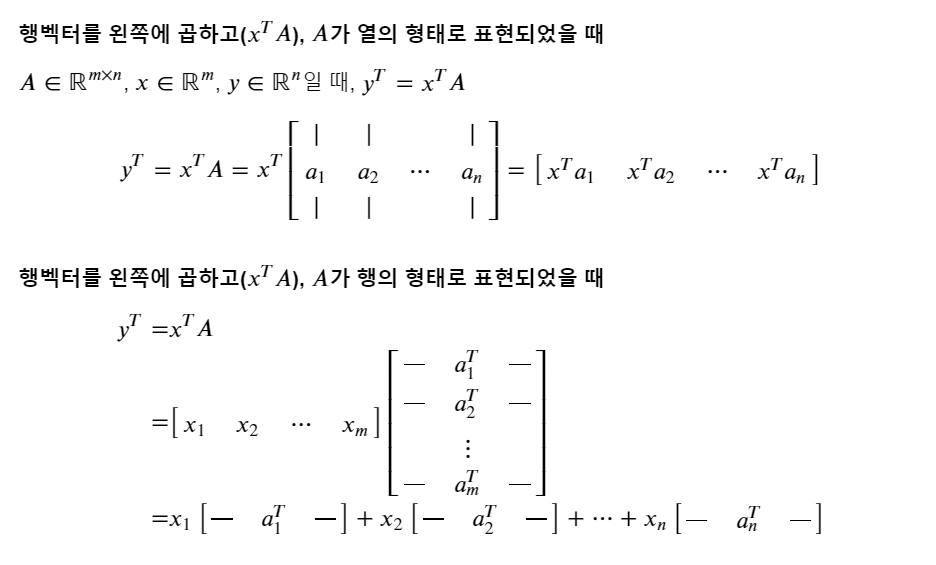
2) 행벡터를 왼쪽에 곱할 때
3. 행렬 x 행렬
가장 많이 사용되는 경우이다.

중요 연산과 성질들
1) 네 가지 종류의 행렬

파이썬에서는 Numpy의 diag함수를 사용하면 대각행렬을 쉽게 생성할 수 있다.
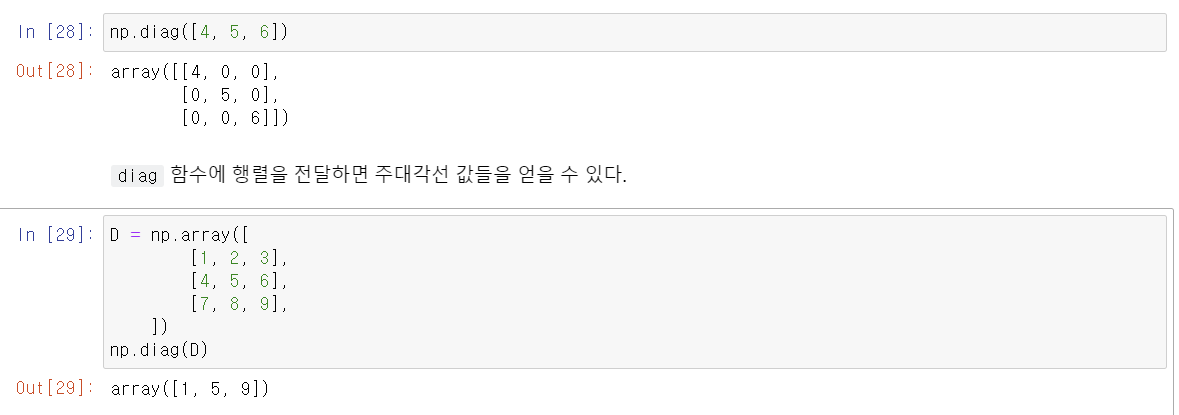
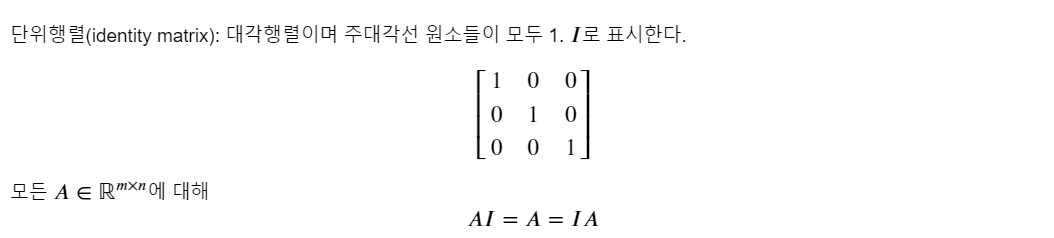
단위행렬 또한 Numpy의 eye 함수를 사용하면 간단하게 단위행렬을 생성할 수 있다.

2) 전치(Transpose) : 행렬 뒤집기

Numpy의 T 속성을 사용하면 행렬을 뒤집을 수 있다.
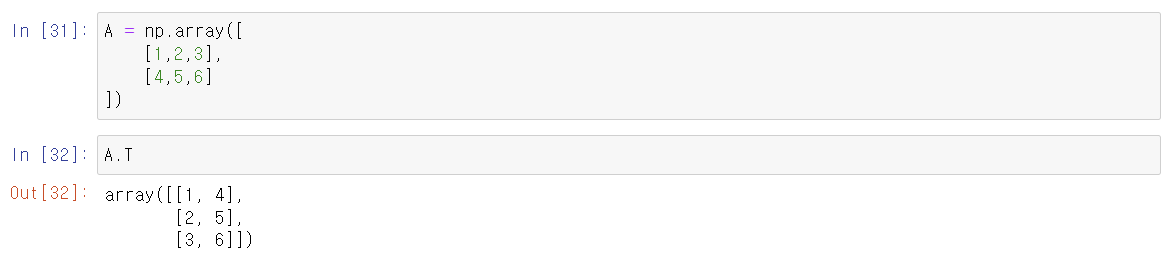
3) 대칭 행렬
- 정방행렬 A와 A의 전치행렬이 동일할 때 : 대칭행렬
- 정방행렬 A와 음의 값 A의 전치행렬이 동일할 때 : 반대칭행렬
대칭행렬은 주대각선을 기준으로 위 아래가 서로 대칭인 모습을 띈다.
A와 A의 전치행렬을 행렬곱하면 대칭행렬의 형태를 나타난다.
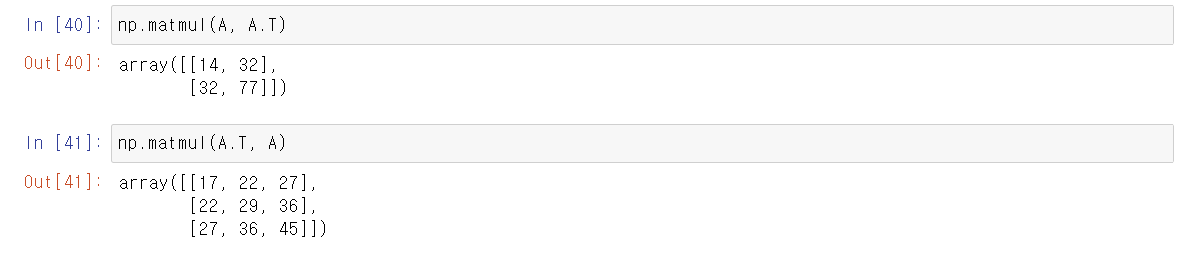
4) 대각합 (Trace)
정방행렬 A의 대각합(주대각선 원소의 합)은 tr(A)로 표기한다.

5) 역행렬(Inverse)
- A의 역행렬이 존재하면, A는 invertible 또는 non-singular 하다고 말한다.
- A의 역행렬이 존재하지 않으면, 선형 종속(Linearly dependent)(어떠한 벡터가 나머지 벡터의 선형조합)이다.

6) 행렬식 (Determinant)
A가 정방행렬일때, A의 행렬식은 다음과 같이 표현한다.
numpy.linalg의 .det 함수를 사용하면 간단히 구해진다.

행렬식이 중요한 점은, 행렬식의 절대값이 행렬 공간 상의 모든 점 집합 S의 부피와 일치한다는 것이다.
A가 역행렬이 존재하지않는 Singular이면, 선형 종속이므로 벡터가 일렬로 나열한 형태가 된다 > 행렬식이 0
이차 형식(Quardratic Forms)
머신 러닝에서 자주 등장하는 식이다.
정방행렬 A와 벡터 x라고 할 때, 이차 형식은 다음과 같다.
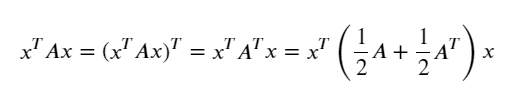
고유값(Eigenvalues)과 고유벡터(Eigenvectors)
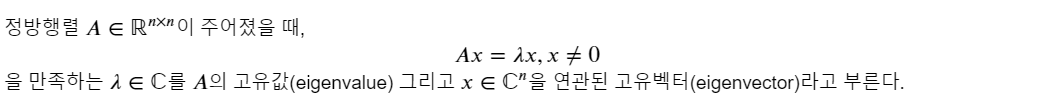
Numpy.linalg의 eig 함수를 사용하면 쉽게 구해진다. (linalg.eig(A) => ( 고유값, 고유벡터 ) 리턴)
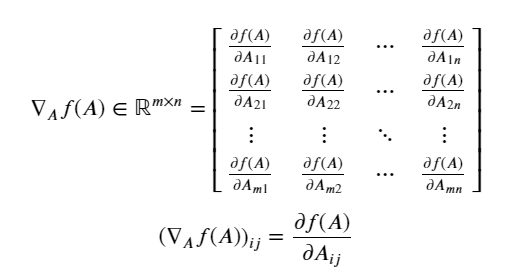
행렬미분 (Matrix Calculus)
최소제곱법(Least Squares)
Ax = b를 만족하는 벡터 x가 없을 경우, Ax가 b에 최대한 가까워지는 x를 찾는 방법
행렬 미분을 통해 풀면,
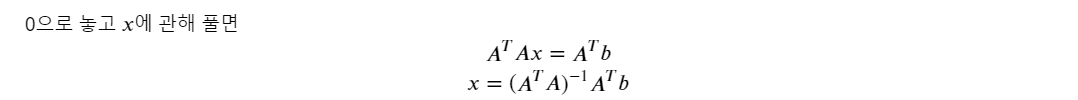
솔직히 하루만에 하기에는 너무 어려웠다ㅠ
'TIL' 카테고리의 다른 글
| Spark 기능과 스케줄링, 메모리 구성 알아보기 - TIL230724 (0) | 2023.07.25 |
|---|---|
| 머신러닝을 위한 확률 기초 - TIL230719 (0) | 2023.07.24 |
| jupyter에서 머신러닝 End to End 실습해보기 - TIL230717 (0) | 2023.07.20 |
| Kafka Producer 및 Consumer 실습해보기 with Python (+ksqlDB) - TIL230713 (0) | 2023.07.14 |
| Kafka 알아보고 설치해보기 - TIL230712 (0) | 2023.07.14 |




