Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
Tags
- disk spill
- Airflow
- spark executor memory
- off heap memory
- aws
- Spark SQL
- AQE
- Spark 실습
- Speculative Execution
- mysql
- SQL
- Docker
- KDT_TIL
- k8s
- Spark
- redshift
- 데이터 파이프라인
- Spark Caching
- Kubernetes
- topic
- DataFrame Hint
- etl
- Spark Partitioning
- Dag
- colab
- Salting
- 빅데이터
- CI/CD
- backfill
- Kafka
Archives
- Today
- Total
JUST DO IT!
[TIL] KDT_20230412 본문
📚 KDT WEEK 2 DAY 3 TIL
- 큐(Queue)
- 이진 트리(Binary Trees)
- 힙(Heaps)
큐(Queue)의 특징
- 선입선출(FIFO)의 자료 구조 "파이포" 라고도 부름
- dequeue 연산의 시간 복잡도 효율을 위해 선형 배열보다 연결리스트가 유리
환형 큐(Circular Queues)의 특징
- 큐의 데이터 사이즈를 제한해두고, 한쪽 끝과 다른 쪽 끝이 맞닿은 형태
- 선형 배열로도 효과적으로 구현 가능

우선순위 큐(Priority Queues)의 특징
- enqueue 연산에 우선순위 순서대로 큐에 데이터를 삽입
- dequue 연산에서 우선순위가 높은 것을 선택할 수도 있겠지만, 이 경우 매 번 O(n) 소요
- 운영체제에서 CPU 스케줄러를 구현할 때 활용됨
이진 트리(Binary Trees)의 특징
- 트리에 포함되는 모든 노드의 차수가 2 이하인 트리
- 정의 자체가 재귀적이기 때문에, 연산들도 대부분 재귀적으로 구현 가능
이진 트리의 깊이 우선 순회
- 중위 순회(in-order traversal) : 왼쪽, 자신, 오른쪽 순서대로 탐색
- 전위 순회(pre-order traversal) : 자신을 먼저 방문 후 왼쪽 탐색, 오른쪽 탐색
- 후위 순회(post-order traversal) : 왼쪽, 오른쪽, 자신 순서대로 탐색
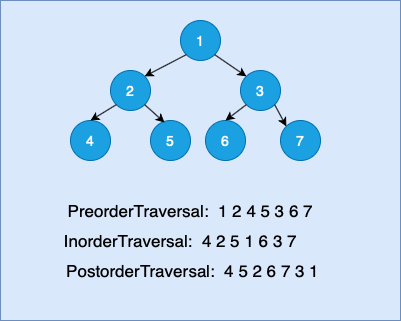
오늘 강좌로 구현했던 코드 예시..
더보기
전위 순회의 경우
def preorder(self):
traversal = []
traversal.append(self.data)
if self.left:
traversal += self.left.preorder()
if self.right:
traversal += self.right.preorder()
return traversal
중위, 후위 순회의 경우 위 코드에서 알맞게 위치만 바꿔줘도 구현이 가능하다.
깊이 우선 순회의 경우 구현이 그렇게 어렵지는 않지만.. 넓이 우선 순회의 경우는 다르다..
이진 트리의 넓이 우선 순회
- 왼쪽부터 오른쪽으로, 낮은 레벨에서 높은 레벨로 차례대로 순회한다.
- 재귀적으로 구현은 어렵고, 큐(Queue)를 활용한 방법이 있다.
구현했던 코드 예시.. 큐를 활용한 방법이 인상적이었다.
더보기
class BinaryTree:
def __init__(self, r):
self.root = r
def bft(self): # 넓이 우선 순회
traversal = []
q = ArrayQueue()
if self.root:
q.enqueue(self.root)
while not q.isEmpty(): # 큐 안에 데이터가 있는 동안은 루프
curr = q.dequeue()
traversal.append(curr.data)
# 왼쪽, 오른쪽 자식이 존재하면 차례로 큐에 넣는다.
if curr.left:
q.enqueue(curr.left)
if curr.right:
q.enqueue(curr.right)
return traversal이렇게 큐에 차례대로 노드를 넣게 되면, 큐의 선입선출에 의해 결국 낮은 레벨 부터 차례대로 탐색하게 된다! 👏
이진 탐색 트리(Binary Search Trees)의 특징
- 왼쪽 서브트리에 자신보다 낮은 값을, 오른쪽 서브트리에 자신보다 높은 값임을 만족하는 트리
- 탐색, 삽입, 삭제의 시간 복잡도가 log(n)에 비례하다. (트리의 좌우 균형이 비슷할 때)
삭제 알고리즘을 구현했던 코드, 생각해 볼 경우의 수가 좀 있었다.
더보기
def remove(self, key):
node, parent = self.lookup(key)
if node:
nChildren = node.countChildren()
# The simplest case of no children
if nChildren == 0:
# 만약 parent 가 있으면
# node 가 왼쪽 자식인지 오른쪽 자식인지 판단하여
# parent.left 또는 parent.right 를 None 으로 하여
# leaf node 였던 자식을 트리에서 끊어내어 없앱니다.
if parent:
if parent.left == node:
parent.left = None
else:
parent.right = None
# 만약 parent 가 없으면 (node 는 root 인 경우)
# self.root 를 None 으로 하여 빈 트리로 만듭니다.
else:
self.root = None
# When the node has only one child
elif nChildren == 1:
# 하나 있는 자식이 왼쪽인지 오른쪽인지를 판단하여
# 그 자식을 어떤 변수가 가리키도록 합니다.
if node.left:
child = node.left
else:
child = node.right
# 만약 parent 가 있으면
# node 가 왼쪽 자식인지 오른쪽 자식인지 판단하여
# 위에서 가리킨 자식을 대신 node 의 자리에 넣습니다.
if parent:
if parent.left == node:
parent.left = child
else:
parent.right = child
# 만약 parent 가 없으면 (node 는 root 인 경우)
# self.root 에 위에서 가리킨 자식을 대신 넣습니다.
else:
self.root = child
# When the node has both left and right children
else:
parent = node
successor = node.right
# parent 는 node 를 가리키고 있고,
# successor 는 node 의 오른쪽 자식을 가리키고 있으므로
# successor 로부터 왼쪽 자식의 링크를 반복하여 따라감으로써
# 순환문이 종료할 때 successor 는 바로 다음 키를 가진 노드를,
# 그리고 parent 는 그 노드의 부모 노드를 가리키도록 찾아냅니다.
while successor.left:
parent = successor
successor = successor.left
# 삭제하려는 노드인 node 에 successor 의 key 와 data 를 대입합니다.
node.key = successor.key
node.data = successor.data
# 이제, successor 가 parent 의 왼쪽 자식인지 오른쪽 자식인지를 판단하여
# 그에 따라 parent.left 또는 parent.right 를
# successor 가 가지고 있던 (없을 수도 있지만) 자식을 가리키도록 합니다.
if successor.left:
child = successor.left
else:
child = successor.right
if parent.left == successor:
parent.left = child
else:
parent.right = child
return True
else:
return False자식의 수부터 시작해서 왼쪽 자식인지.. 오른쪽 자식인지.. 등 구별해야 한다.
힙(Heaps)의 특징
- 루트 노드가 항상 최대값, 최솟값을 가지느냐에 따라 최대힙, 최소힙으로 나뉜다.
- 서브트리 또한 최대힙이나 최소힙의 조건을 만족해야 한다.
- 완전히 크기 순서대로 정렬되어 있진 않으나, 힙 정렬(Heap sort) 알고리즘을 통해 정렬에 사용된다.
- 삽입, 삭제 시간에 log(n) 만큼 소요한다.
- 노드의 추가와 삭제가 항상 마지막 원소에서만 일어난다. ➡ 완전 이진 트리를 만족해야 하기 때문!
🤔 공부하면서 어려웠던 내용
오늘만 세 가지의 자료구조를 배웠다..😂
각 자료구조의 특징이 뚜렷하고 쓰임새가 보여서 재밌긴 했었지만..
이 구조들을 알맞은 상황에 딱딱 사용하려면 정말 많은 문제를 풀어보는 게 답인 것같다..🤤
'TIL' 카테고리의 다른 글
| [TIL]KDT_20230417 (0) | 2023.04.17 |
|---|---|
| [TIL] KDT_20230414 (0) | 2023.04.14 |
| [TIL] KDT_20230413 (0) | 2023.04.13 |
| [TIL] KDT_20230411 (0) | 2023.04.11 |
| [TIL] KDT_20230410 (0) | 2023.04.10 |


